BENFORD’S LAW
Benford’s Law which is also called as Newcomb-Benford’s law and first digit law was first stated by an astronomer Simon Newcomb in 1881 but later in 1938 it was stated by a physicist Frank Benford. This law can be used to detect fraud in various statistical data as it analyses the distribution frequency of first digit in the data.
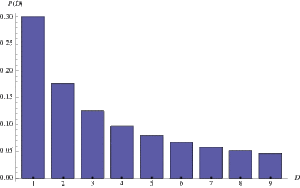
It simply states that if we select a number randomly from a given statistical data, the probability of first digit to be 1 is 0.301 in spite of it being 0.1 (as calculated through general probability laws). This can also be demonstrated by a general observation i.e. If you take the front page of a newspaper and encircle all the numbers in that page, your calculation will show that about 30% of the numbers start with the digit 1. The law states that the probability of first digit to be “d” is:-
ln(10)
Each bar represents a digit, and the height of the bar is the percentage of numbers that start with that digit.
Benford’s Law is applicable to almost all uniformly distributed data but it has an exception in certain cases:
· Telephone directories do not obey the law as most of the numbers do not have their initial digit as 1.
· Square root and Reciprocals.
· All the data which do lie in a range whose initial digits do not start with 1.
Besides this the law is applicable to a wide variety of statistical data like addresses, stock prices, population, etc.
By
Mridul Upreti